문제 요약
입력값으로 get, add의 명령어와 더불어서 name, score의 리스트가 주어집니다. add 명령에 따라 name, score의 리스트를 순차적으로 넣되 get하는 시점에는 add한 것들 중 아래의 규칙대로 뽑아 반환합니다.
- score는 큰 순으로, 만약 같다면 name이 사전 정렬식으로 뽑는다
- n번째 get을 할 때 뽑는 것도 앞에서부터 n번째 것을 뽑는다
해결
이 문제를 해결할 때 중점둬야 하는 것이 2가지 있습니다. 하나는 정렬이 필요하다는 것이고, 또 하나는 뽑을 때는 n번째로 뽑는 것을 가능한 빠르게 뽑아야 한다는 것입니다. 정렬을 하는 것은 흔하게 하는 것이다보니 크게 고민할 필요가 없으나, 그에 더불어서 n번째의 것을 뽑는 것은 좀 고민해봐야 하는 포인트였습니다.
여기서 기발한 아이디어는 java에서 heap을 구현하는 PriorityQueue를 2개를 쓰는 것입니다. 하나는 min heap으로, 또 하나는 max heap으로 말이죠.
public SORTracker() {
minPriorityQueue = new PriorityQueue<>();
maxPriorityQueue = new PriorityQueue<>(Collections.reverseOrder());
}
public void add(String name, int score) {
minPriorityQueue.offer(new Location(name, score));
maxPriorityQueue.offer(minPriorityQueue.poll());
}
public String get() {
Location location = maxPriorityQueue.poll();
minPriorityQueue.offer(location);
return location.name;
}add할때는 min heap에서 넣었다가 max heap으로 넣어주고, get할때는 max heap에서 꺼낸다음 min heap으로 다시 넣어줍니다. 물론 꺼낸 것에서 값은 반환하구요.
이게 어떻게 해서 가능한 걸까요? 문제를 좀 더 단순화해서 그냥 일반 숫자라고 그림으로 표현해볼게요.
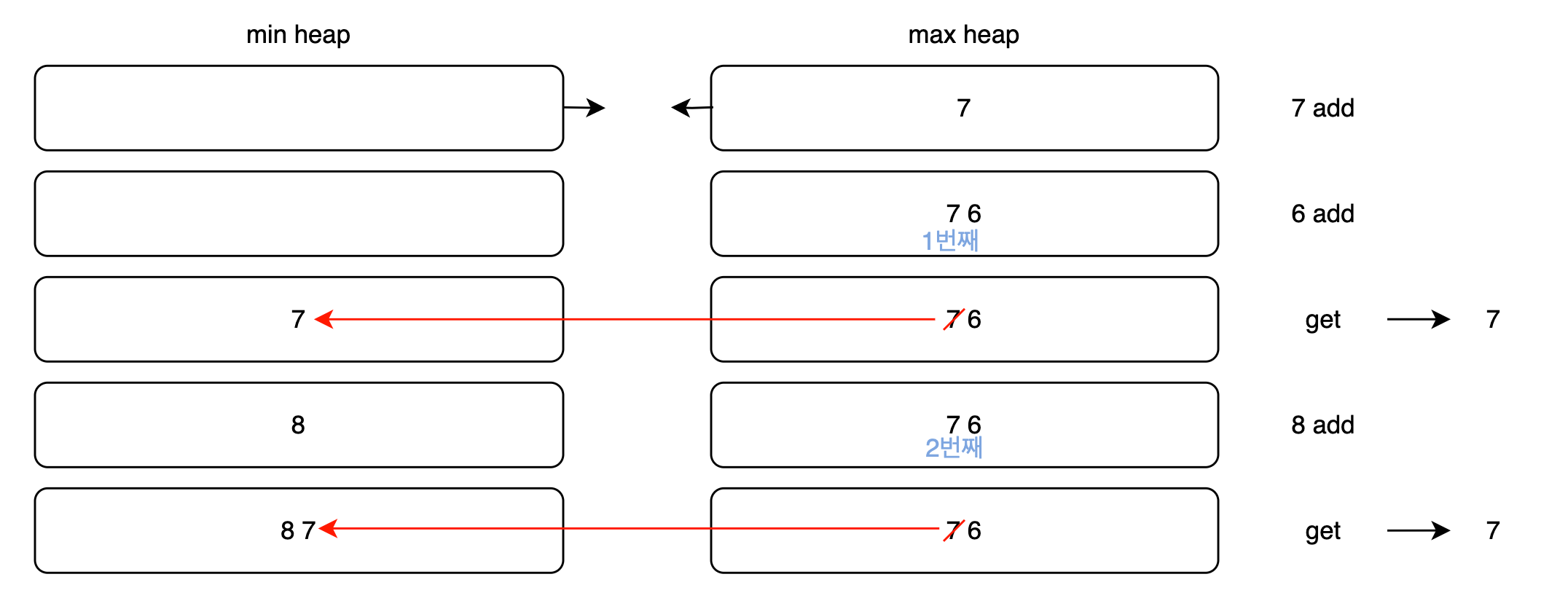
min heap을 뽑을 때 오른쪽으로 뽑고, max heap은 왼쪽 순으로 뽑는다고 편의상 생각해볼게요. 여기서 max heap과 min heap의 역할 차이가 나옵니다.
| min heap | max heap |
| n번째 뽑아야 할 후보를 max heap으로 넘겨줌 | heap 내 정렬 기준대로 뽑도록 준비 |
그림을 보면 min heap, max heap에 걸쳐서 몇 번째의 것을 뽑으면 되는지 눈에 보입니다. min heap은 n번째 뽑아야 할 후보를 max heap으로 넘겨주는 중요한 역할을 합니다. 예를 들어 위 그림에서 첫번째 get의 경우 7을 빼어 그 당시 2번째 뽑으면 되는 6을 제일 우선순위 높게됩니다. 하지만 그 후 8이 들어오고 나서 2번째 뽑을 순위가 다시 7이 되어 버렸죠. min heap이 이미 1개가 get이 된 상황에서 그 중 get하게 될 후보가 8보다는 7이 다시 가는게 적합하다고 판단한거죠(물론 min heap에 따를 뿐이지만 역할로 따진다면). 이렇게 add할 때마다 무조건 적합한 후보 하나는 max heap으로 꼭 보내기 때문에 get을 개수만큼 하면 부족함없이 모두 잘 뽑히게 됩니다.
교훈
max heap, min heap 2개를 동시에 써서 (정렬 + n번째의 요소 꺼내기)는 기발하고 재밌는 아이디어였습니다. 어느정도 특수한 조건이라고 생각되어서 변형 문제가 크진 않을 것 같긴한데 비즈니스 로직 구현 할때도 일부 유용하게 써볼 수는 있을 것 같네요. min heap, max heap으로 특수한 문제를 창의적으로 해결할 수 있다는 아이디어를 얻었습니다. 그리고 기본 자료구조의 여러가지 조합도 또 다시 나오면 알아두면 유용하겠다는 생각이 들었습니다.
'Algorithm > problem solving' 카테고리의 다른 글
| leetcode 452. Minimum Number of Arrows to Burst Balloons (0) | 2023.03.29 |
|---|---|
| leecode 253. Meeting Rooms II (0) | 2023.03.20 |
| Today's Algorithm(2020-11-23) (1) | 2020.11.23 |
| Today's Algorithm(2019-03-20) (2) | 2019.03.20 |
| Today's Algorithm(2019-03-18) (0) | 2019.03.18 |
