문제 요약
여러개의 포인트(시작점, 끝점)들이 주어지고 화살을 쏠 때, 여러 포인트들을 모두 맞추는 최소의 화살 개수를 구하는 문제였습니다.
이 문제는 부분에 대한 최적의 해를 구하다보면 전체의 최적의 해에도 도달하는 Greedy Algorithm 문제였습니다.
Greedy Algorithm (탐욕 알고리즘)
탐욕 알고리즘이란 그 당시(부분)의 최적의 해를 쫓아 최종적인 해답에 도달하는 방법을 말합니다. 이렇게 해결할 수 있는 문제는 2가지 특징이 있습니다.
- 부분의 최적의 해를 쫒아 선택한 것은 그 다음 선택에 영향을 주지 않는다
- 최종적인 해답은 부분의 대한 최적의 해답들로 이루어진다
사실 Greedy Algorithm은 문제 풀 당시에는 '그냥 이렇게 하면 되지 않을까?'(이게 이 당시 최적 아닐까?) 하면서 접근을 하게되고, 그게 작용하면 'Greedy하게 풀 수 있구나'라고 나중에 생각을 하게 되는 것 같습니다.
해결
이 문제의 핵심은 끝을 기준점을 둬야 한다는 것입니다.
그럼 왜 끝을 기준점을 둬야할까요?
그 이유는 끝이 이 문제에서 최적의 해를 도달하기 위한(Greedy한) 방법을 제시하기 때문입니다. 끝을 기준점을 둘 때 그 다음 시작점과 제대로 비교를 할 수 있습니다.
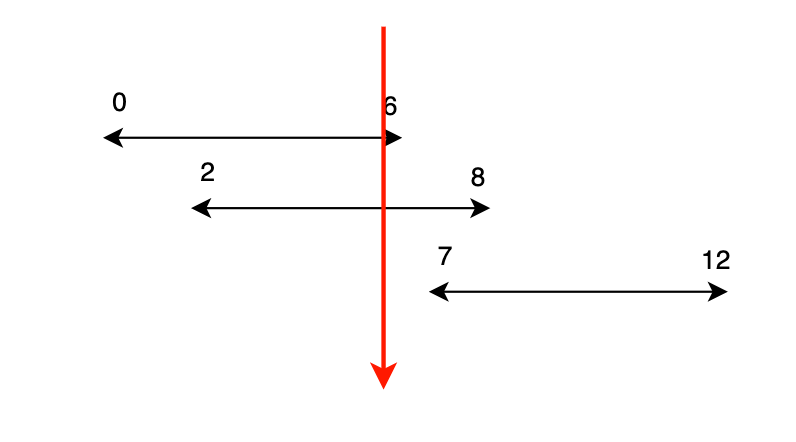
예를들어 (0, 6), (2, 8), (7, 12)가 주어졌을 때 6이 기준이 되어야 이 당시에 2개를 다 도달할 수 있는 최적의 해인 것입니다. 물론 (2, 8), (7, 12) 사이에 8을 기준으로 고려할 수 있습니다. 하지만 정렬기준을 위에서 내려온다고 할 때 (0, 6), (2, 8)의 최적을 구하는 것과 (7, 12)의 최적을 구하는 것은 기준점이 다르기 때문에 별도로 보는 것이 맞습니다. 이 기준점에서 볼 때 이 문제는 끝을 정렬하여 풀 수 있습니다.
public int findMinArrowShots(int[][] points) {
Arrays.sort(points, (p1, p2) -> p1[1] < p2[1] ? -1 : 1);
int end = points[0][1];
int answer = 1;
for(int i = 1; i < points.length; i++) {
if(points[i][0] <= end) {
continue;
}
answer++;
end = points[i][1];
}
return answer;
}끝을 기준으로 정렬을 한 후 그 다음의 시작점이 작거나 같을 때는 그냥 넘어갑니다(부분에서의 최적의 해). 만약 시작점이 더 크다면 현재 최적의 해의 범위를 벗어나므로 그 때는 그 다음 최적의 해를 구합니다.
물론 꼭 끝으로만 정렬해야 하는 건 아닙니다.
public int findMinArrowShots(int[][] points) {
Arrays.sort(points, (p1, p2) -> p1[0] < p2[0] ? -1 : 1);
int end = points[0][1];
int answer = 1;
for (int i = 1; i < points.length; i++) {
if(points[i][0] <= end) {
end = Math.min(end, points[i][1]);
continue;
}
answer++;
end = points[i][1];
}
return answer;
}시작점 기준으로 정렬하되 그 다음 포인트의 비교하기 위한 끝점을 제대로 다시 설정해주면 됩니다.
교훈
문제의 핵심이 무엇인지 알면 그것에 도달하기 위한 방법은 다양합니다. 문제를 해결하지 못해 해답을 보더라도 그 문제의 핵심이 무엇인지, 왜 그게 핵심이 인지 이해하는 것이 중요하다는 것을 다시 깨닫습니다.
'Algorithm > problem solving' 카테고리의 다른 글
| leetcode 907. Sum of Subarray Minimums (0) | 2023.05.01 |
|---|---|
| leetcode 2444. Count Subarrays With Fixed Bounds (0) | 2023.05.01 |
| leecode 253. Meeting Rooms II (0) | 2023.03.20 |
| leetcode 2102. Sequentially Ordinal Rank Tracker (0) | 2023.03.19 |
| Today's Algorithm(2020-11-23) (1) | 2020.11.23 |
